Cuboctahedron
Read here about a polyhedron that is significant to tensegrity geometry.
Cuboctahedron
The cuboctahedron is one of the Archimedean polyhedra. It can be conceived as formed of truncating a cube or octahedron.
Tensegrity Structures that Conform with the Cuboctahedron
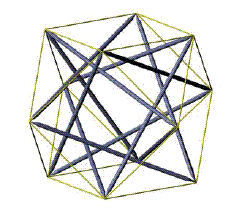
Motro described a tensegrity structure where the continuum of cables is exactly mapped to the edges of a Cuboctahedron. He wrote, “There are four triangular compressed components. Each of them constitutes a circuit of struts (a circuit is a particular case of chain). These triangles are intertwined and their equilibrium is ensured simultaneously by a hexagon of cables and the effect of the three other triangles for three of the apices of each hexagon.
Gómez Jáuregui classes the cuboctahedron-like tensegrity structure as a “circuit” configuration structure. He wrote, “the compressed components are conformed by circuits of struts, closing the rhombus generated by the struts and cables of the diamond pattern tensegrities. Several regular and semiregular polyhedra can be built related to this class, e.g. cuboctahedron, icosidodecahedron, snub cube, snub icosahedron, etc.” In his illustration below, the cuboctahedron is composed of 4 circuits of 3 struts (every circuit interweaving with each other) and the cables defining the edges of the polyhedron.
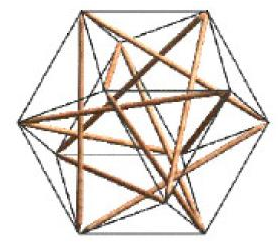
Pugh proposed a tensegrity structure consisting of 4 compressed triangles held within a 24 member tensile network.
Moelman described a tensegrity structure that outlined a cuboctahedron with 6 struts and 24 tensile vectors.
Cuboctahedron as a significant form in energetic-synergetic geometry
Cuboctahedron as closest sphere packing
In close packing of spheres, imagine a vertex at each sphere's nucleus. Imagine these vertices connected by struts. The form described by these vertices and struts is a cuboctahedron.
Cuboctahedron as maximum-volume state of the Jitterbug
When the Jitterbug is allowed to expand to its maximum volume, it describes a cuboctahedron. As the jitterbug collapses, the square faces of the cuboctahedron become rhombic and then close completely.
Cuboctahedron as the ideal state of the isotropic vector matrix (IVM)
The IVM is formed by filling allspace with cuboctahedra.